PointFlow: 3D Point Cloud Generation with Continuous Normalizing Flows

PointFlow: 3D Point Cloud Generation with Continuous Normalizing Flows

Abstract
As 3D point clouds become the representation of choice for multiple vision and graphics applications, the ability to synthesize or reconstruct high-resolution, high-fidelity point clouds becomes crucial. Despite the recent success of deep learning models in discriminative tasks of point clouds, generating point clouds remains challenging. This paper proposes a principled probabilistic framework to generate 3D point clouds by modeling them as a distribution of distributions. Specifically, we learn a two-level hierarchy of distributions where the first level is the distribution of shapes and the second level is the distribution of points given a shape. This formulation allows us to both sample shapes and sample an arbitrary number of points from a shape. Our generative model, named PointFlow, learns each level of the distribution with a continuous normalizing flow. The invertibility of normalizing flows enables computation of the likelihood during training and allows us to train our model in the variational inference framework. Empirically, we demonstrate that PointFlow achieves stateof- the-art performance in point cloud generation. We additionally show that our model can faithfully reconstruct point clouds and learn useful representations in an unsupervised manner.
Video
Brief Introduction to the Method
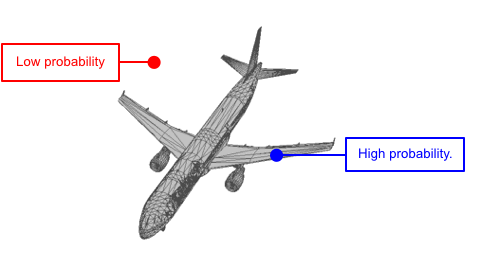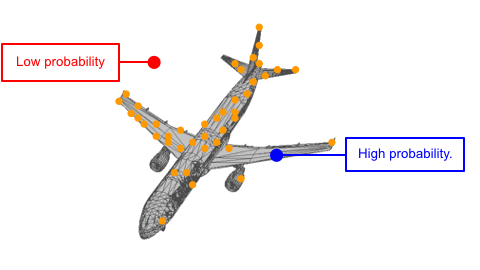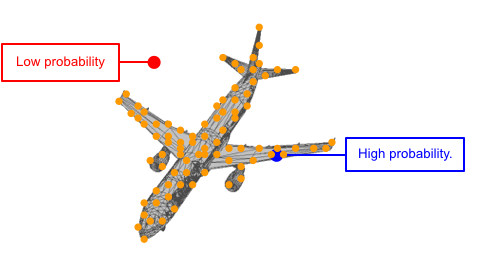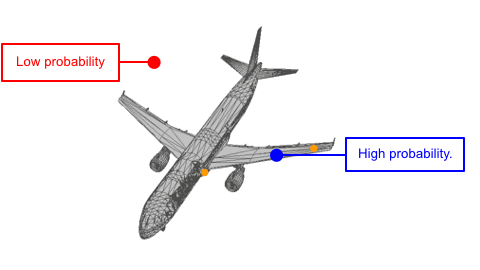
Each shape can be viewed as a distribution of 3D points. In such distribution, points on the shape have higher probability and are more likely to be sampled. A point cloud can be viewed as a set of points sampled from such distribution.
We use two continuous normalizing flows (CNFs) to model the distribution of shapes, while each shape is a distribution of 3D points. The latent CNF transforms a vector sampled from the shape prior to a latent shape vector. The point CNF transforms 3D points sampled from the point prior to a point cloud conditioned on a shape vector.
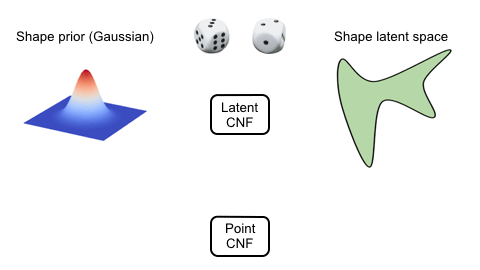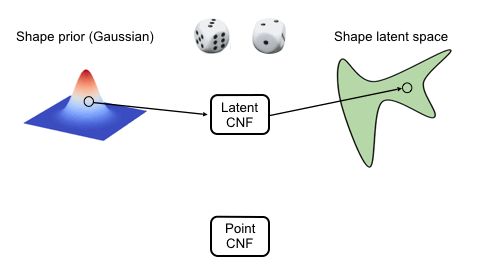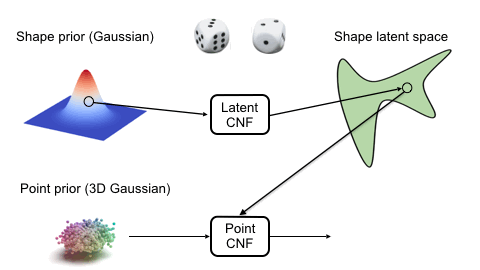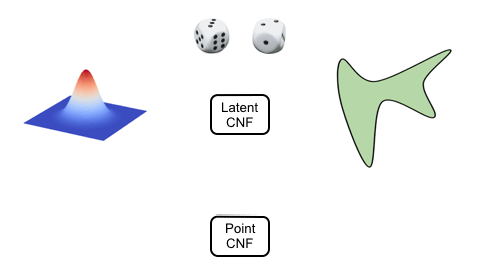
Visulaization of the Flow
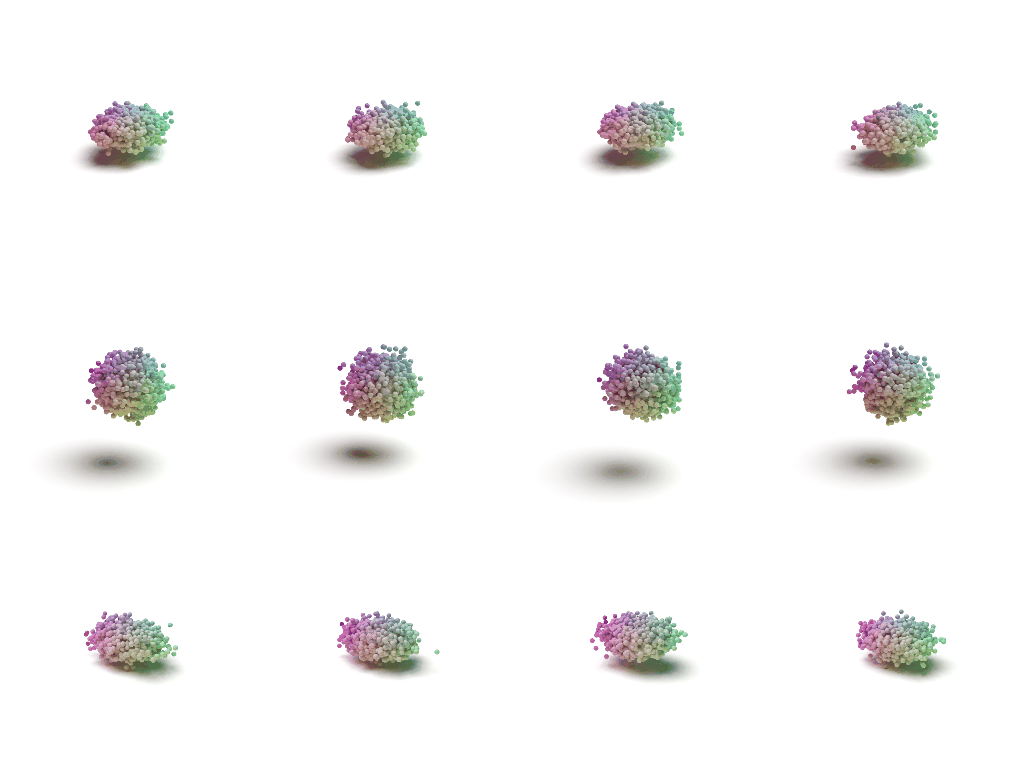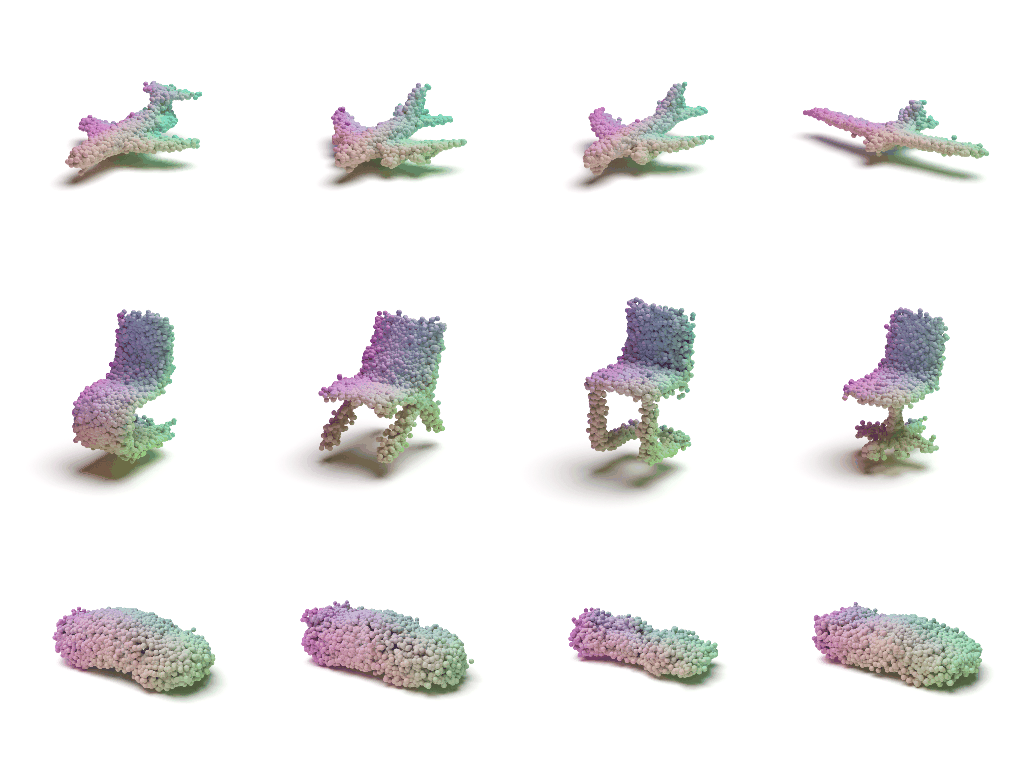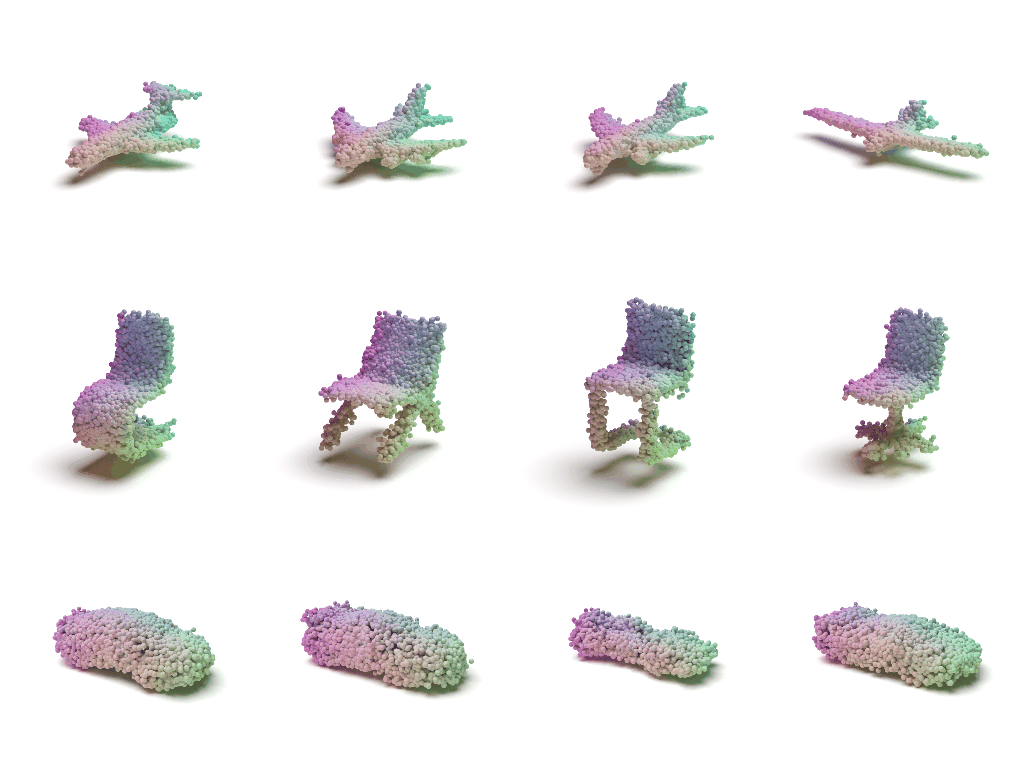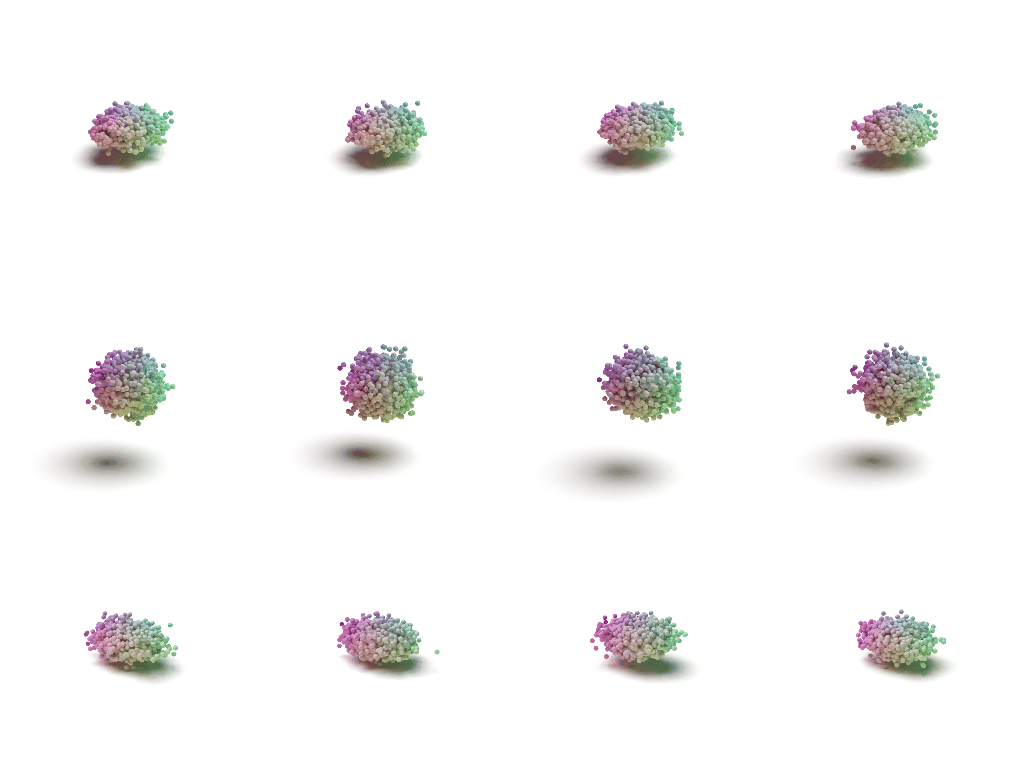
Acknowledgements
This work was supported in part by a research gift from Magic Leap. Xun Huang was supported by NVIDIA fellowship.