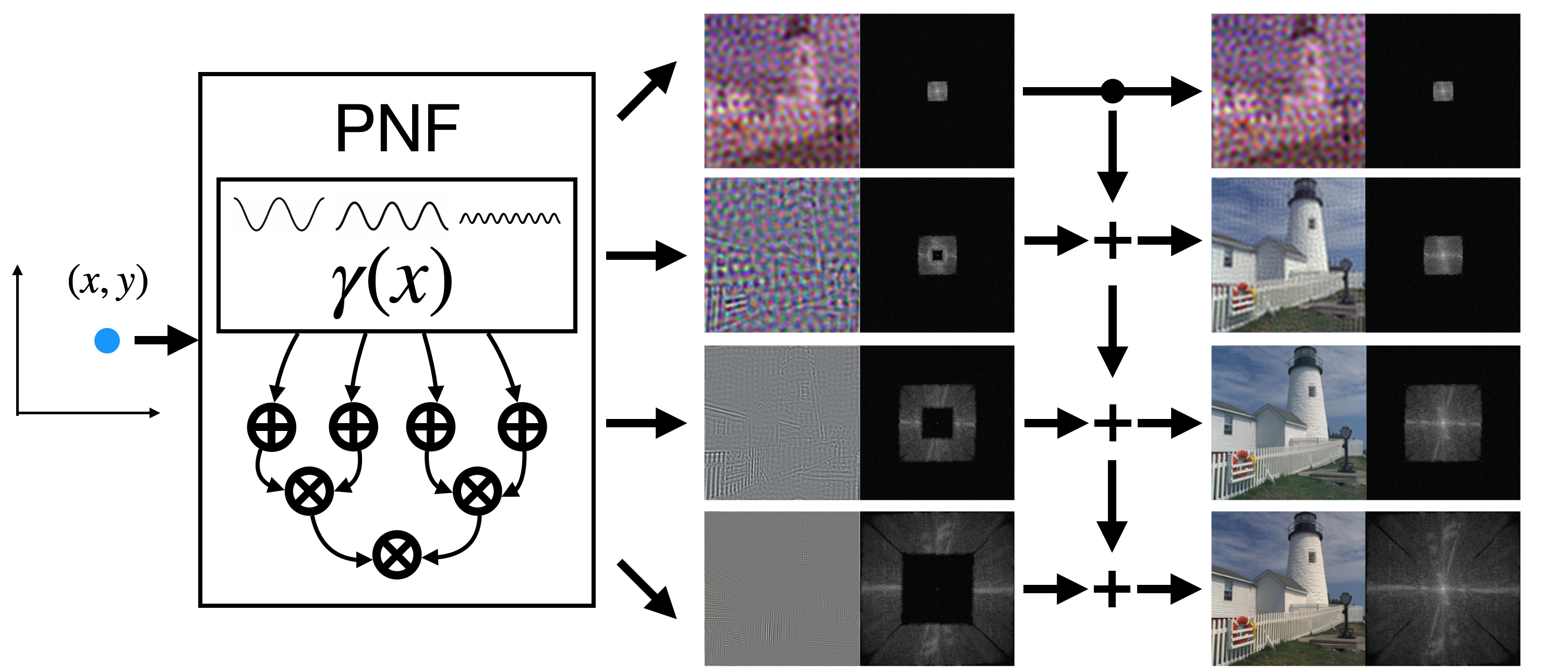
Neural fields have emerged as a new paradigm for representing signals, thanks to their ability to do it compactly while being easy to optimize. In most applications, however, neural fields are treated like a black box, which precludes many signal manipulation tasks. In this paper, we propose a new class of neural fields called basis-encoded polynomial neural fields (PNFs). The key advantage of a PNF is that it can represent a signal as a composition of a number of manipulable and interpretable components without losing the merits of neural fields representation. We develop a general theoretical framework to analyze and design PNFs. We use this framework to design Fourier PNFs, which match state-of-the-art performance in signal representation tasks that use neural fields. In addition, we empirically demonstrate that Fourier PNFs enable signal manipulation applications such as texture transfer and scale-space interpolation.