Geometry Processing with Neural Fields
Geometry Processing with Neural Fields

Abstract
Most existing geometry processing algorithms use meshes as the default shape representation. Manipulating meshes, however, requires one to maintain high quality in the surface discretization. For example, changing the topology of a mesh usually requires additional procedures such as remeshing. This paper instead proposes the use of neural fields for geometry processing. Neural fields can compactly store complicated shapes without spatial discretization. Moreover, neural fields are infinitely differentiable, which allows them to be optimized for objectives that involve higher-order derivatives. This raises the question: can geometry processing be done entirely using neural fields? We introduce loss functions and architectures to show that some of the most challenging geometry processing tasks, such as deformation and filtering, can be done with neural fields. Experimental results show that our methods are on par with the well-established mesh-based methods without committing to a particular surface discretization.
Video
Introduction
This paper advocate using neural fields for geometry processing tasks. Neural fields are neural networks that maps spatial coordinates to signals (e.g. a sign distance field). Our goal is to perform geometry processing tasks directly on neural fields without extracting meshes.
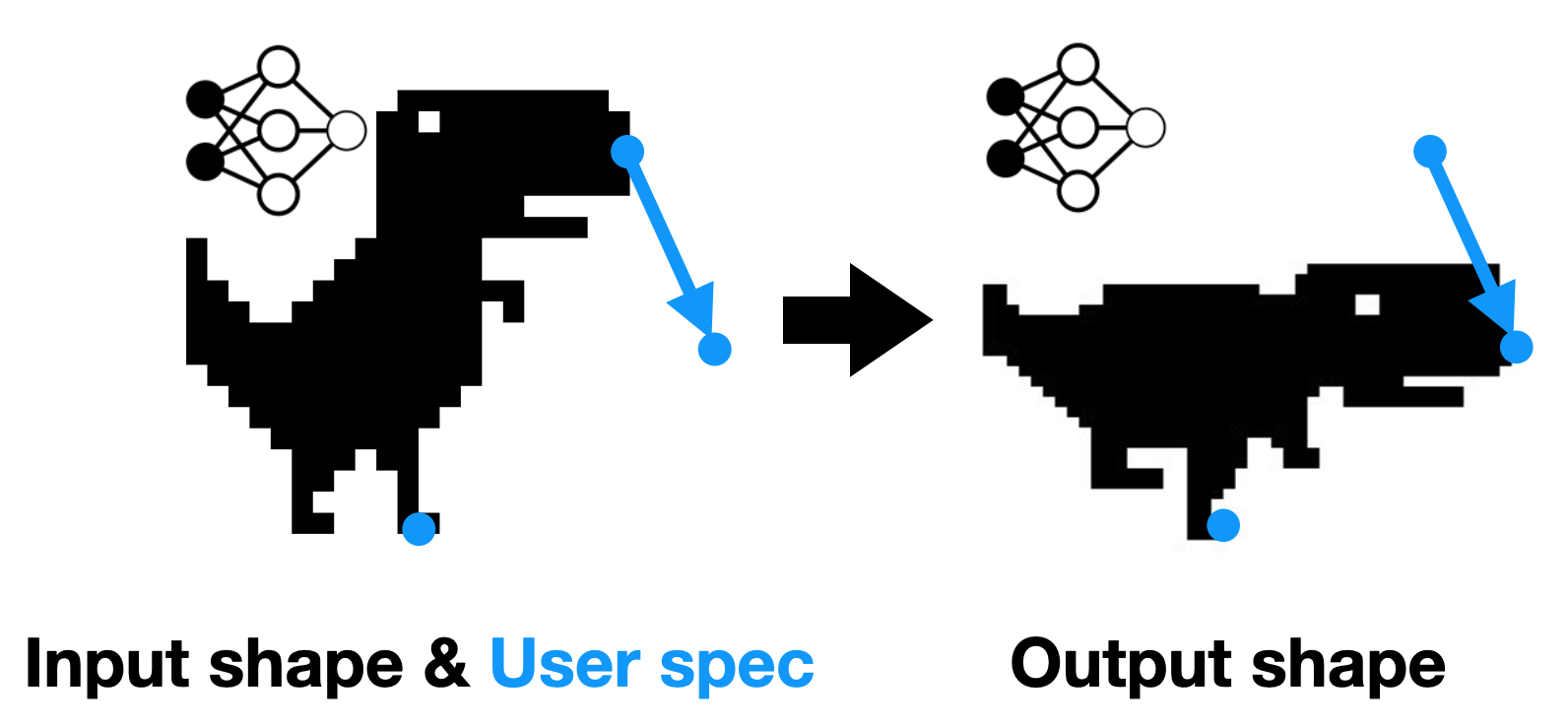
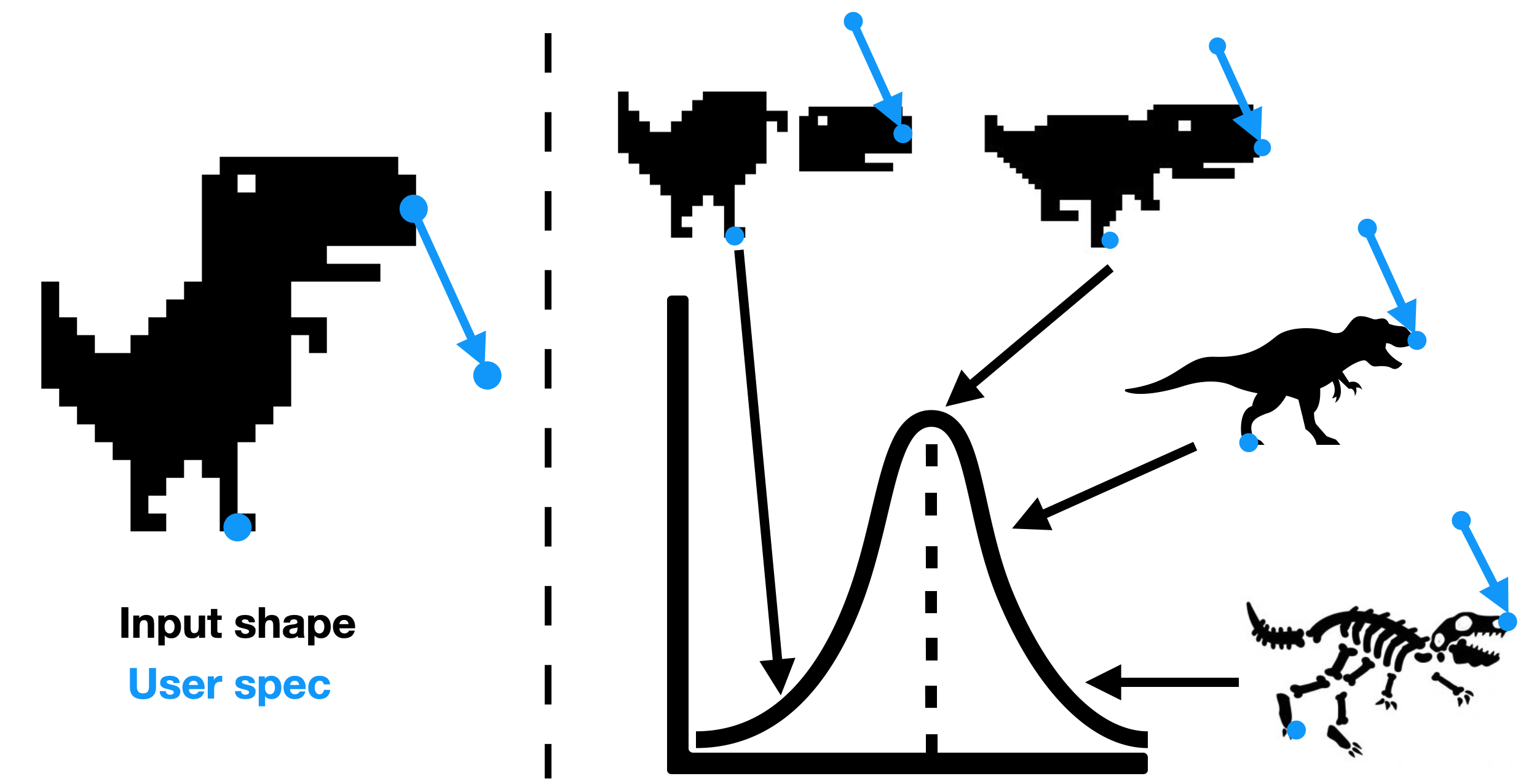
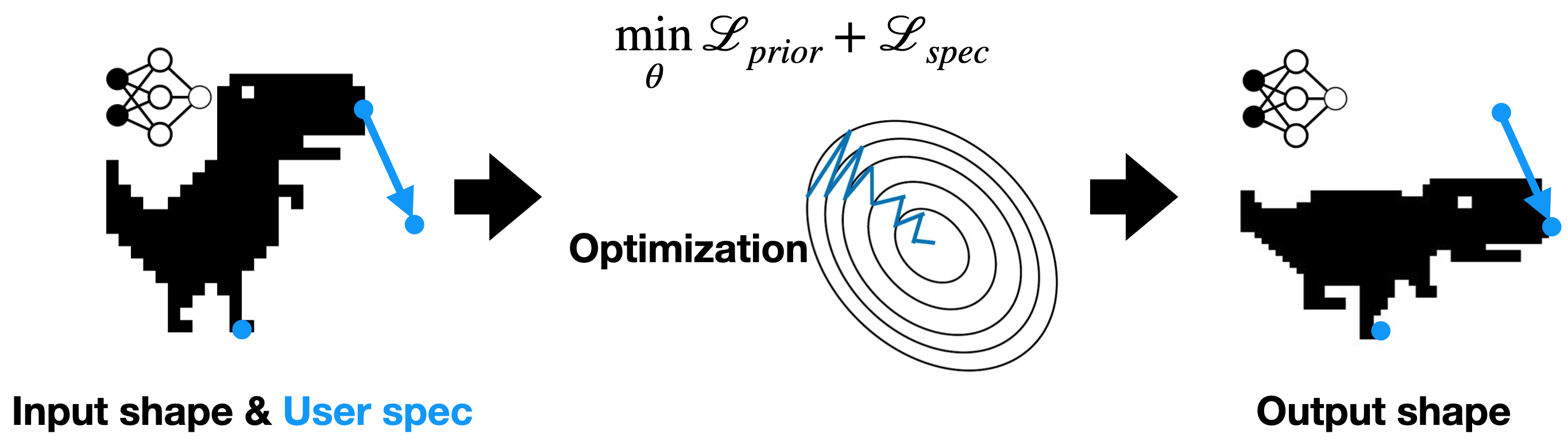
Geometry processing is an under-constrainted problem because the user specification is usually sparse. There might exist multiple valid solution to the same input shape and user specification. As a result, we need to encode a prior to select the most reasonable outputs. In this paper, we will show how to encode physics inspired priors using neural fields.
Deformation
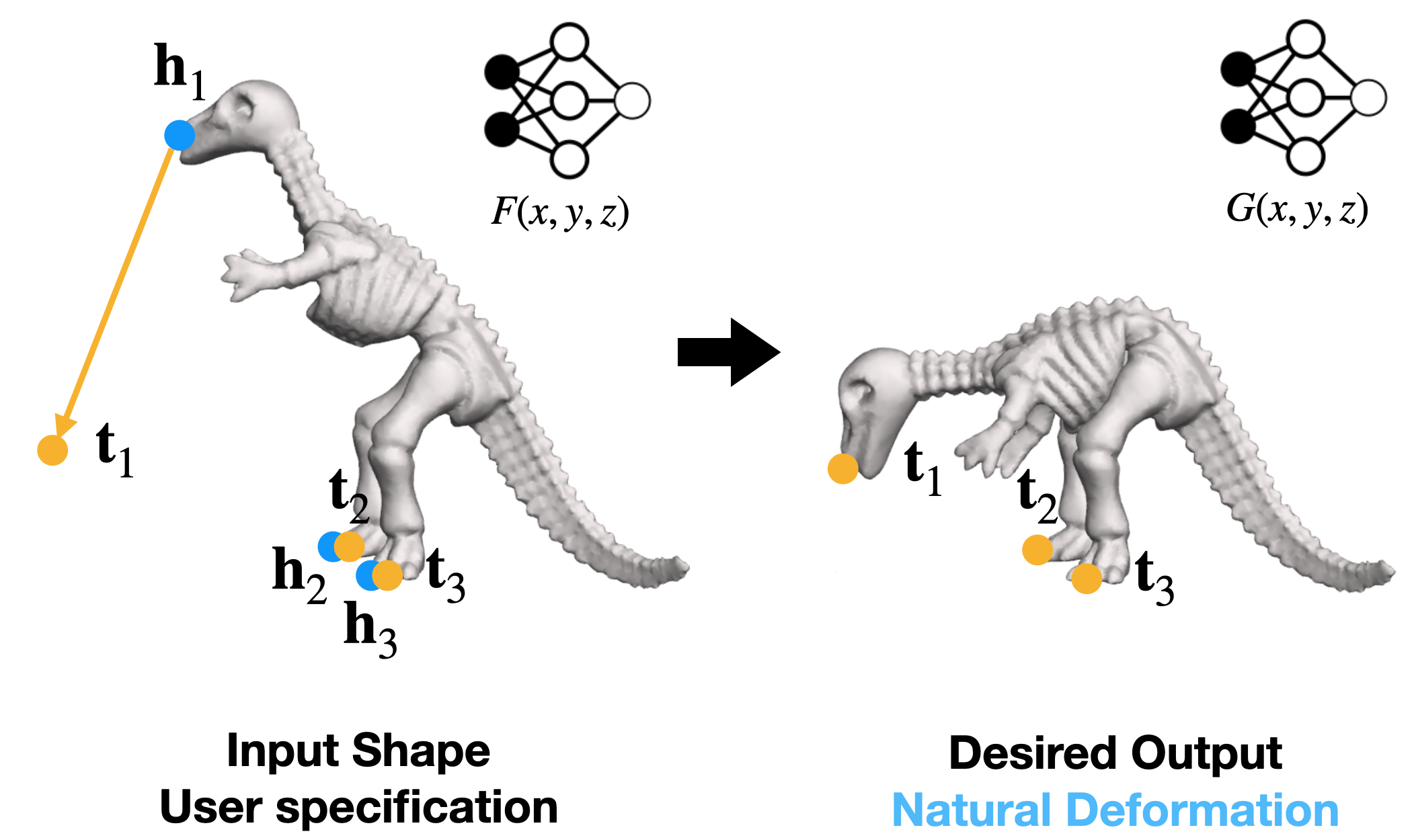
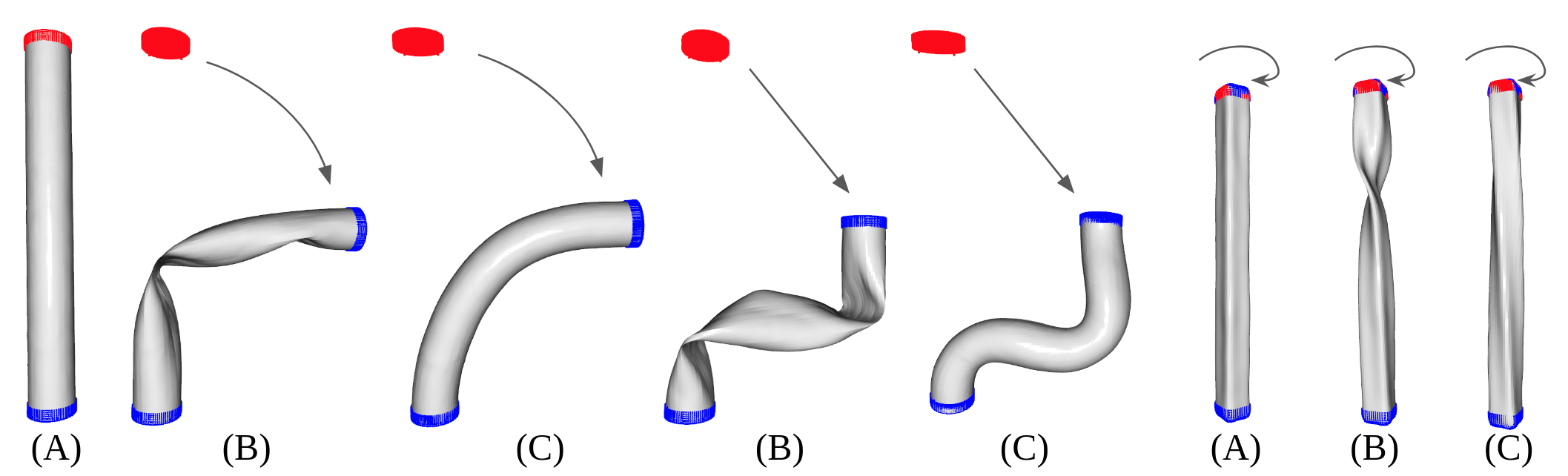
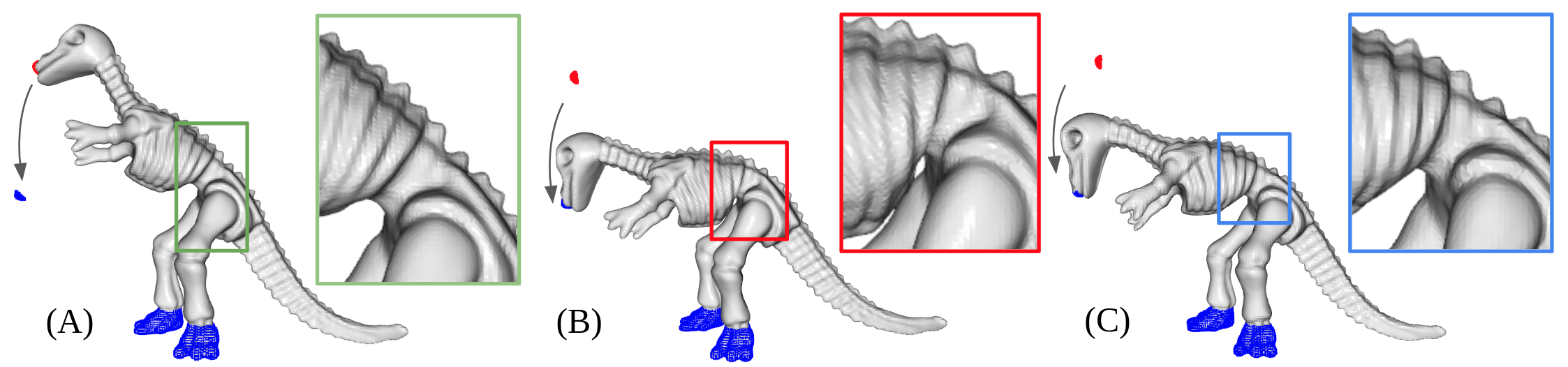
The goal of this task is to deform the input shape in a way that both fulfills user specs and resembles natural deformation. User will specify a set of points as handles (i.e. the blue points). The user can either move the handle or keep it unchanged. Natural deformations are those that can happen in real world objects.
One type of natural deformation is elastic deformation, which assume the material has some resistence to bending and stretching. We develop training objectives to prior our model to learn elastic deformation.
Following are the results for deformation. (A) Showing handles and targets in the original shapes; (B) Using ARAP directly on mesh extracted from the input neural field using marching cube; (C) Our results.
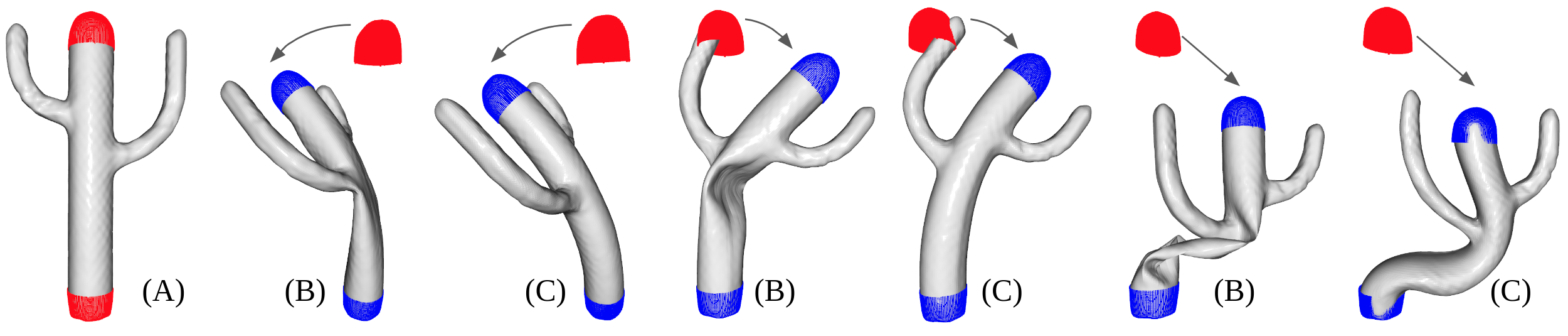
Our model (i.e. C) can optimize for multiple handles (e.g. both hands and foot):

Our model (i.e. C) tends to create less volume distortion as we can see in the zoom-in region:
Acknowledgements
Guandao’s PhD was supported in part by a research gift from Magic Leap and a donation from NVIDIA. We want to thank Wenqi Xian, Professor Steve Marschner , and members of Intel Labs for providing insightful feedback for this project.